Password Strength is Relative to Attack Algorithm
Passwords are everywhere in our technology laden world. The number of accounts a single person has grows constantly (I sign up for a new web site or service at least once a month). Because of this, it’s of ever-increasing importance to be smart about how you secure your accounts and choose passwords with a high password strength.
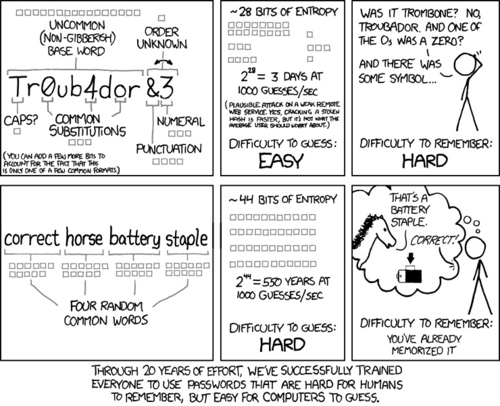
The webcomic XKCD had an eye-opening issue a while back, which I believe has been hotly debated in various forums:
There are two concepts Munroe is focusing on here: the difficulty for an attacking program to guess a password, and the difficulty for a human being to remember the password. Already we can see how password strength is relative to your perspective, but it gets better.
The comic expresses password strength in terms of entropy, which is essentially a measure of many attempts it would take an attacking program to correctly guess the password. In the comic, the gray boxes represent “bits” of entropy, which describe the maximum number of attempts required to find the password in terms of $ 2^n$, where $ n$ is the number of entropy bits.
I’m willing to accept Munroe’s argument for the difficulty of remembering the passwords in his examples without dispute. When it comes to the difficulty of guessing the passwords, well - I wouldn’t say I dispute what he says - it’s just harder to digest what he’s putting out there. So let’s take a closer look.
Password Strength of the “Troubador” Method
First, let’s look at the entropy bits he attributes to the difficult to remember password:
- Sixteen bits for the choice of an uncommon (non-gibberish) word.
- One bit because the first character may or may not be capitalized.
- Three bits because certain letters may or may not be swapped with numbers (a la “leet speak”).
- Four bits for the special symbol at the end of the password.
- Three bits for the number at the end of the password.
- One bit because the order of the special symbol and the number at the end of the password might be switched.
Let’s get the easy ones out of the way first. Assigning one bit to the capitalization of the first letter and one to the order of the last two characters makes perfect sense. $ 2^1 = 2 $, which means figuring out whether the first character is capitalized or not takes a maximum of two guesses. Remember, at this point we’re not worried about figuring out what that first letter is; the probabilities for guessing that are satisfied by some of the other entropy bits.
The next easy ones are the bits assigned to the number and special character at the end of the password. If we’re talking about a single digit, then we’re looking at $ 10 \approx 2^3 $ choices. It’s not exact, but we can see that Munroe is erring on the conservative side.
Next, the common substitutions. Here, we are given three entropy bits, but why? That gives us about eight choices, or three choices between two things (notice how he’s adding one entropy bit per possible replacement even though one character is still a letter and not a digit). I’m not sure how you’d represent the average entropy of this practice. You’d need to calculate the average number of digit-replaceable letters in any given word. For every letter like this, you have a two-way choice - is it the letter, or was it replaced with a digit? Three possible letter swaps in a word seems reasonable enough to me.
Finally, the entropy bits assigned to the word itself. Munroe is saying that a dictionary of uncommon words has about $ 2^{16} = 65,536$ words in it. A quick search reveals that there are well over a hundred thousand words in the English language, so it seems reasonable that a word list expansive enough to contain uncommon words would probably be something over fifty thousand.
Upon closer examination, I’m satisfied with the entropy bits assigned to this method of password generation. How about Munroe’s second method?
Password Strength of the “Battery Staple” Method
Here, there is only one rule:
- Eleven bits assigned to each common word used in the password.
Already, we can see that there is a difference between common and uncommon words. The difference is about five bits of entropy, to be more precise. So a dictionary of common words might contain $ 2^{11} = 2,048$? I can believe that. It is interesting to note, though, what a huge difference those five bits make. Still, when four of these common words are used together, the entropy adds up pretty quickly.
What’s the Catch?
So Munroe’s approach appears to hold water, however I still have one big misgiving. Assigning the entropy bits in this fashion makes the assumption that an attacker approaches the problem armed with the knowledge of the algorithm that was used to generate the password. What if an attacker used a simple brute force method that just tried every combination of letters, numbers, and special characters? There are twenty six letters, but really fifty two because lowercase and capital letters are different. There are ten digits, and let’s stick with Munroe’s four entropy bits (sixteen) possible choices for special characters.
Using this simple brute force method, every character of the password has $ 78 \approx 2^6$ possibilities. That means the method one password (11 characters long) now has sixty six bits of entropy. That’s higher than the forty four bits Munroe assigned to the password generated by the second method. At the same time, what if we used the same simple brute force attack on the second password. It’s got twenty five characters, and so would have one hundred and fifty bits of entropy.
I doubt anyone actually uses such a basic brute force algorithm anymore (who knows!), but it’s an easy way to illustrate the fact that a given password’s entropy is relative to the method used to attack it. In my example, Munroe’s second password was still the stronger of the two, but, there could be other algorithms that might render that password relatively weak.
In the end, what can we do to increase the password strength on our accounts? The two key points brought up by the comic very clearly describe where we want to be: passwords that are easy for humans to remember, but hard for computers to guess. The question remains - how exactly do we do that when the actual strength of the password against an attack is relative to the attack algorithm? For me, I’ll stick with the battery staple, at least I can remember it.

About Adam Platt
Adam Platt is a technologist with more than a decade of experience across the full stack. His passion for technology and penchant for rendering complex technical ideas into simple terms have made him an in-demand speaker. His resume includes BriForum, the PowerShell Summit, teaching engagements and more.
He is one of the 10 types of people who understand binary and he can solve a Rubik’s Cube.

About Adam Platt
Adam Platt is a technologist with more than a decade of experience across the full stack. His passion for technology and penchant for rendering complex technical ideas into simple terms have made him an in-demand speaker. His resume includes BriForum, the PowerShell Summit, teaching engagements and more.
He is one of the 10 types of people who understand binary and he can solve a Rubik’s Cube.